G₂ manifold

In differential geometry, a G₂ manifold is a seven-dimensional Riemannian manifold with holonomy group G₂. The group 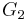is one of the five exceptional simple Lie groups. It can be described as the automorphism group of the octonions, or equivalently, as a proper subgroup of SO(7) that preserves a spinor in the eight-dimensional spinor representation or lastly as the subgroup of GL(7) which preserves a positive, nondegenerate 3-form, 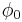. The later definition was used by R. Bryant. Non-degenerate may be taken to be one whose orbit has maximal dimension in 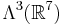. The stabilizer of such a non-degenerate form necessarily preserves an inner product which is either positive definite or of signature 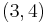. Thus, 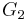is a subgroup of 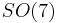. By covariant transport, a manifold with holonomy 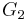has a Riemannian metric and a parallel (covariant constant) 3-form, , the associative form. 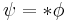The Hodge dual, is then a parallel 4-form, the coassociative form. These forms are calibrations in the sense of Harvey-Lawson, and thus define special classes of 3 and 4 dimensional submanifolds, respectively. The deformation theory of such submanifolds was studied by McLean.

Properties

If M is a 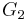-manifold, then M is:

• Ricci-flat
• orientable
• a spin manifold

History

Manifold with holonomy 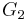was firstly introduced by Edmond Bonan in 1966, who constructed the parallel 3-form, the parallel 4-form and showed that this manifold was Ricci-flat. The first complete, but noncompact 7-manifolds with holonomy 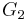were constructed by Robert Bryant and Salamon in 1989. The first compact 7-manifolds with holonomy 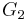were constructed by Dominic Joyce in 1994, and compact 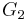manifolds are sometimes known as "Joyce manifolds", especially in the physics literature.

Connections to physics

These manifolds are important in string theory. They break the original supersymmetry to 1/8 of the original amount. For example, M-theory compactified on a 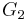manifold leads to a realistic four-dimensional (11-7=4) theory with N=1 supersymmetry. The resulting low energy effective supergravity contains a single supergravity supermultiplet, a number of chiral supermultiplets equal to the third Betti number of the 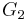manifold and a number of U(1) vector supermultiplets equal to the second Betti number.

See also: Calabi-Yau manifold, Spin(7) manifold

References

• E. Bonan, (1966), "Sur les variétés riemanniennes à groupe d'holonomie G2 ou Spin(7)", C. R. Acad. Sci. Paris 262: 127–129 .
• Bryant, R.L. (1987), "Metrics with exceptional holonomy", Annals of Mathematics (Annals of Mathematics) 126 (2): 525–576, doi:10.2307/1971360, JSTOR 1971360 .
• Bryant, R.L.; Salamon, S.M. (1989), "On the construction of some complete metrics with exceptional holonomy", Duke Mathematical Journal 58: 829–850 .
• Harvey, R.; Lawson, H.B. (1982), "Calibrated geometries", Acta Mathematica 148: 47–157, doi:10.1007/BF02392726 .
• Joyce, D.D. (2000), Compact Manifolds with Special Holonomy, Oxford Mathematical Monographs, Oxford University Press, ISBN 0-19-850601-5 .
• McLean, R.C. (1998), "Deformations of calibrated submanifolds", Communications in Analysis and Geometry 6: 705–747 .
• Karigiannis, Spiro (2011), "What Is . . . a G₂-Manifold?", AMS Notices 58 (04): 580–581, http://www.ams.org/notices/201104/rtx110400580p.pdf .